Question

Given f(x) = x, if g(x) = f(x) + 4. What would happen to the graph? A. The line will become steeper and will move up 4. B. The line will become steeper and will move down 4. C. The line will become less steep and will move up 4. D. The line will become steeper and will move down 4.

Answer 1

Functions can be transformed the same way as points or figures in the coordinate system.

If you add a determined value "d" to a function, it translates into a vertical translation upwards d units.

If you subtract "d" to a function, it translates into a vertical translation downwards d units.

`f(x)\to g(x)=(1)/(2)f(x)+4`

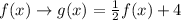
In this case, given the function

`f(x)=x`

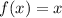
If you add 4 units to the function, the function will move "up" 4 units.

As mentioned, this is a translation, the form of the functions are not changed, just their positions in the coordinate plane and the lines will be parallel.

Next, the function f(x)is multiplied by 1/2.

The transformation is a dilation.

Given a scale factor "a"

If |a|>0, the result is a vertical stretch, the line becomes steeper.

If |a|<0, the result is a vertical compression, the line becomes less steep.

So f(x) was compressed 1/2 and moved 4 units up.

The correct option is C.