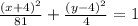Question

uestion 7of 10 Step 1 of 1ind the equation of the ellipse with the following properties. Express your answer in standard form.Centered at (-4, 4)Major axis of length 18 oriented verticallyMinor axis of length 4swer 2 Points

Answer 1

Answer:
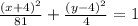
`((x+4)^(2))/(81)+((y-4)^(2))/(4)=1`Step-by-step explanation:

The center of the ellipse, (h, k) = (-4, 4)

The length of the major axis = 18

The length of the semi-major axis, a = 18/2 = 9

The length of the minor axis = 4

The length of the semi minor axis, b = 4/2 = 2

The equation of the ellipse is calculated as shown below

`((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1`

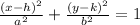
Substitute h = -4, k = 4, a = 9, and b = 2 into the equation

`\begin{gathered} ((x-(-4))^2)/(9^2)+((y-4)^2)/(2^2)=1 \\ \\ ((x+4)^2)/(81)+((y-4)^2)/(4)=1 \end{gathered}`

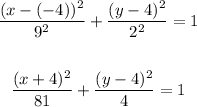
Therefore, the equation of the ellipse is:

`((x+4)^(2))/(81)+((y-4)^(2))/(4)=1`