Question

A data set lists earthquake depths. The summary statistics are n=600, x=6.38 km, s=4.52 km. Use a 0.01 significance level to test the claim of a seismologist that these earthquakes are from a population with a mean equal to 6.00. Assume that a simple random sample has been selected. Identify the null and alternative hypotheses, test statistic, P-value, and state the final conclusion that addresses the original claim.

Answer 1

Given:

• n = 600

,

• x' = 6.38 km

,

• s = 4.52 km

,

• Population mean, x = 6.00

Let's solve for the following:

• (a). What are the null and alternative hypotheses?

The null hypothesis will be: H₀: μ = 6.00 km

The alternative hypothesis will be: H₁: μ ≠ 6.00 km

Thus, we have:

H₀: μ = 6.00 km

H₁: μ ≠ 6.00 km

• (b). Determine the test statistic.

To find the test statistic, apply the formula:

`t=(x^(\prime)-\mu)/((s)/(√(n)))`

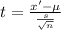
Thus, we have:

`\begin{gathered} t=(6.38-6.00)/((4.52)/(√(600))) \\ \\ t=(0.38)/(0.1845) \\ \\ t=2.059\approx2.06 \end{gathered}`

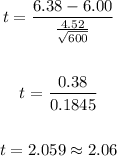
Therefore, the test statistic is 2.06

• (c). Determine the P-value.

This is a two-tailed test.

Where:

Significance level, α = 0.01

Degrees of freedom, df = n - 1 = 600 - 1 = 599

With a test statistic of 2.06.

To find the P-value, we have:

`t_(0.01,599)=0.0398\approx0.04`

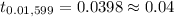
The P-value is 0.04.

• (d). State the final conclusion:

Since the P-value is less greater the significance level (0.01), we fail to reject the null hypothesis H0.

Fail to reject H₀. There is insufficient evidence to conclude that the mean of the population of earthquake depths is 6.00 km is not correct.

ANSWER:

• (a). A. H₀: μ = 6.00 km

H₁: μ ≠ 6.00 km

• (b). test statistic = 2.06

• (c). P-value = 0.04

• (d). ,Fail to reject, H₀. There is ,insufficient, evidence to conclude that the mean of the population of earthquake depths is 6.00 km ,is not, correct.