Question

Find the volume of the compass. It is a half cylinder laying on its side in the bottom is a rectangular prism.

Answer 1

The image consist of half of a cylinder and a rectangular prism. The following parameters that were given are;

`\begin{gathered} radius(r)\text{ }of\text{ cylinder}=5\text{ }inches \\ length\text{ of prism =10 inches} \\ breadth\text{ of prism =6 inches} \\ height\text{ of prism=8 inches} \\ hight\text{ of cylinder =6 inches} \end{gathered}`

Step-by-step explanation

To find the volume of the composite shape, we will combine the formula for the rectangular prism and the half cylinder.

`\begin{gathered} Volume\text{ of rectangular prism = }l* b* h_p \\ Volume\text{ of half cylinder }=(1)/(2)\pi r^2h_c \end{gathered}`

Therefore, we will have;

`\begin{gathered} Volume\text{ of composite shape =}lbh_p+(1)/(2)\pi r_^2h_c \\ Volume=(10*6*8)+(0.5*\pi*5^2*6) \\ Volume=480+75\pi \\ Volume=480+235.61944 \\ Volume=715.61944 \end{gathered}`

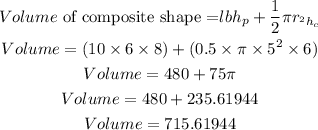
Answer: 715.61944 Cubic inches