Question

Need help with this problem One solutionNo solutions Infinitely many solutions

Answer 1

To determine the number of solutions, we have to solve each equation for x.

1.- To solve the equation for x, first, we apply the distribute property on both sides of the equation:

`2x-14=-3x+18.`

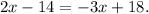
Adding, 3x to both sides of the equation, we get:

`\begin{gathered} 2x-14+3x=-3x+18+3x, \\ 5x-14=18. \end{gathered}`

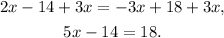
Adding 14 we get:

`\begin{gathered} 5x-14+14=18+14, \\ 5x=32. \end{gathered}`

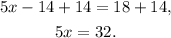
Dividing by 5, we get:

`x=(32)/(5)\text{.}`

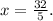
Therefore, the equation has one solution.

2.- Applying the distributive property on the right side of the equation, we get:

`14-3x-5=3x+9.`

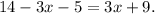
Adding like terms, we get:

`9-3x=3x+9,`

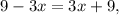
therefore, by properties of real numbers,

`x=0.`

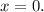
The equation has 1 solution.

3.- Applying the distributive property on the right side of the equation, we get:

`12x-1=12x-6.`

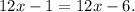
Subtracting 12x from both sides of the equation, we get:

`\begin{gathered} 12x-1-12x=12x-6-12x, \\ -1=-6. \end{gathered}`

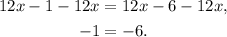
The above equality is a contradiction, therefore the equation has no solutions.

4.- Applying the distributive property on the left side of the equation, we get:

`x+5x=6x\text{.}`

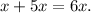
Simplifying the above equation, we get:

`6x=6x\text{.}`

Since the above equality is always true for any value of x, then the equation has infinitely many solutions.

5.- Applying the distributive property on the left side of the equation, we get:

`36-8x-2x=8-10x\text{.}`

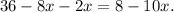
Adding like terms, we get:

`36-10x=8-10x\text{.}`

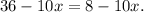
Adding 10x to both sides of the equation, we get:

`\begin{gathered} 36-10x+10x=8-10x+10x, \\ 36=8. \end{gathered}`

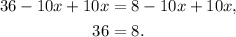
The above equality is a contradiction, therefore the equation has no solutions.