Question

A cam goer wanted to estimate the average price of sleeping bags in a resort area he normaly visits. He collected prices (in $) of a random sample 20 sleeping bags from shops in this area. The data is given below. Assume that the population of prices of sleeping bags in this resort area has an approximately normal distribution.95, 120, 40, 120, 115, 65, 30, 25, 100, 110, 105,100, 105, 95, 110, 120, 95, 90, 70, 100Use software (or your calculator) to find the mean (x bar) and standard deviation (s) of the prices of the above sample. (Round your answers to two decimal places.)a. x = $[a]b. s = $[b] Using the given data as representative of the population of prices of all sleeping bags, find a 99% confidence interval for the mean price μ of all sleeping bags. (Round your answers to two decimal places.)c. lower limit = $[c] d. upper limit = $[d]

Answer 1

• a) $90.50

,

• b) $29.29

,

• c) $73.63

,

• d) $107.37

Step-by-step explanation

Given the data, we can calculate the mean and standard deviation using a software.

• a)

That software will use the following formula for the mean:

`\bar{x}=\frac{sum\text{ of all observations}}{total\text{ number of observations}}`

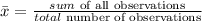
In our case, we have 20 observations, meaning:

`\bar{x}=(95+120+40+...+90+70+100)/(20)=90.5`

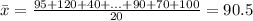
• b)

Similarly, for the standard deviation s the formula is:

`s=\sqrt{\frac{\sum_^(x-\bar{x})}{n-1}}`

where x represents each observation.

Then, using the software we would get:

`s\approx29.29`

Finally, the confidence interval (CI) can be calculated using the following formula:

`CI=\bar{x}\pm Z*(s)/(√(n))`

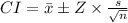
Replacing the data we get:

`CI=90.5\pm2.5758*(29.29)/(√(20))\approx90.5\pm16.87`

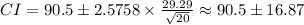
Meaning that the upper limit will be:

`90.5+16.87=107.37`

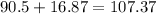
While the lower will be:

`90.5-16.87=73.63`