Question

Determine which expressions represent purely real numbers and which expressions represent non-real complex numbers.
`7 - 5i`
`- i {}^(2) + i ^(3)`
`\sqrt{( - 5) ^(2) }`
`i ^(6)`
`0 + 9i`
`√( - 6)`
`2 - {7i}^(2)`
`- 12`

Answer 1

We have the next numbers and we need to classify them in purely real numbers and non-real complex numbers.

for

7-5i - it is a non-real complex number because we have an imaginary number

for

`-i^2+i^3`

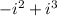
we need to reduce the expression above

`-i^2+i^3=1-i`

as we can see the expression is a non-real complex number because we have an imaginary number.

For

`\sqrt[]{(-5)^2}`

we need to simplify the expression

`\sqrt[]{(-5)^2}=5`

as we can see we have purely real number

For

`i^6=i^2\cdot i^2\cdot i^2=-1\cdot-1\cdot-1=-1`

as we can see we have a purely real number

For

`0+9i`

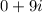
we have a non-real complex number

For

`\sqrt[]{-6}=i\sqrt[]{6}`

if we have inside a square root a negative number the result will be a non-real complex number.

For

`2-7i^2=2-7(-1)=2+7=9`

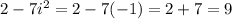
as we can see we have a purely real number

for

-12 we have a purely real number