Question

Consider the following graph.Step 1 of 2: Does the graph represent a function?A103sAnswerKeypadKeyboard ShortcutsO YesO No

Answer 1

YES

Explanations:

What is a function?

A function is a relation in which every input value in the domain has a distinct value in the codomain. This means that for every value of x, there must be a corresponding value of "y"

The given curve is a parabola. The equation of a parabola is quadratic in nature. From the graph, you can see that the curve intersects the x-axis at two points (at x = 1.5 and x = 4.5)

The factors will be (x - 1.5) and (x - 4.5). Taking the product of the factors;

`\begin{gathered} f(x)=(x-1.5)(x-4.5) \\ f(x)=x^2-4.5x-1.5x+6.75 \\ f(x)=x^2-6x+6.75 \end{gathered}`

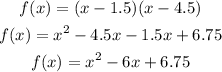
Since the resulting expression is a quadratic function, hence the given graph represents a function.

We can also check by using the vertical line test. The vertical lines rule states that if a vertical line drawn across the graph intersects the graph in NOT more than one point, hence it is a function otherwise it is not.

If vertical lines are drawn on this graph, it will not intersect the graph at more than one point showing that the graph represents a function.