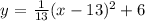The general equation of a parabola with vertex (h,k) is

In our case, we have h = 13 and k =6. So we get the equation

Now, to find the value of C, we will use the given y intercept. In the previous equation we should get y=19 if we replace x = 0. So
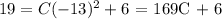
If we subtract 6 on both sides, we get
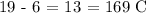
If we divide both sides by 169, we get
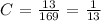
So the general equation of the given quadratic function is