Given
The initial investment is given 5000 dollar , interest rate is 7.5 percent per year compounded quarterly.
Required
To determine the time required to grow the initial investment of 5000 dollar to 6800 dollar.
Step-by-step explanation
The formula for the amount ,

For compounded quarterly , n=4.
Substitute the values.
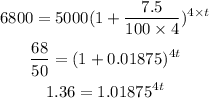
Take ln both sides.
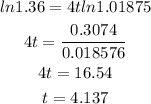
Answer
Hence the time required for an investment of 5000 dollars to grow to 6800 dollars at an interest rate of 7.5 percent per year, compounded quarterly is 4.14 years.