Question

A company manufacturers and sells a electric drills per month. The monthly cost and price-demand equations areC(x) = 75000 + 70x,P= 160 - x/30 , 0 < 2 < 5000.(A) Find the production level that results in the maximum profit.Production Level =(B) Find the price that the company should charge for each drill in order to maximize profit.Price =

Answer 1

Given the cost and demand functions:

`\begin{gathered} C(x)=75000+70x \\ p(x)=160-(x)/(30) \\ 0\leq x\leq5000 \end{gathered}`

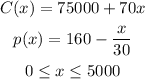
we can find the revenue with the following expression:

`R(x)=xp(x)=160x-(x²)/(30)`

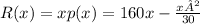
then, the profit can be calculated with the difference between the revenue and C(x):

`P(x)=R(x)-C(x)=160x-(x²)/(30)-75000-70x=90x-(x²)/(30)-75000`

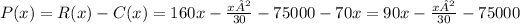
to find the max profit, we can find the derivative of P(x) and find its root to get the value of x that maximizes the function P(x):

`\begin{gathered} P(x)=90x-(x²)/(30)-75000 \\ \Rightarrow P^(\prime)(x)=90-(2)/(30)x=90-(1)/(15)x \\ P^(\prime)(x)=0\Rightarrow90-(1)/(15)x=0 \\ \Rightarrow(1)/(15)x=90 \\ \Rightarrow x=90*15=1350 \\ x=1350 \end{gathered}`

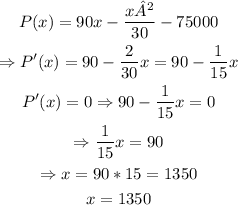
therefore, the production level that results in the maximum profit is x = 1350.

Finally, to find the price, we can evaluate x = 1350 on p(x):

`p(1350)=160-(1350)/(30)=160-45=115`

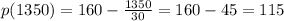
therefore, the price that the company should charge for each drill to maximize profit is $115