A car travels 10 km southeast.
The illustration will be :
The angle to the vertical line of southeast is 45 degrees.
Next is 15 km in a direction 60 degrees north of east.
Updating the illustration above.
From the vertical line, the angle is 60 degrees.
The resultant vector is a straight line at starting point to the final point.
And we will form a triangle :
Note that the red marked angle is congruent to 45 degrees.
So the total angle of the vertex is 45 + 60 = 105.
Now using cosine law in finding the third side of a triangle :
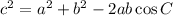
where c = third side
a and b = other two sides
C = angle opposite to the third side.
So we have :
a = 10, b = 15 and angle C = 105 degrees.
Substitute the given values :
![\begin{gathered} c^2=10^2+15^2-2(10)(15)\cos 105 \\ c^2=402.64571 \\ c=\sqrt[]{402.64571} \\ c=20.1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/k1agpfvaga4ojvgxnemss87b41aheknd3r.png)
ANSWER :
20.1 km