Question

Let f(x) = x^2 + 8x.a) Evaluate f(-3). b) Solve f(x)= -16.

Answer 1

`a)f(-3)=-15,b)x=-4`

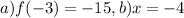
1) Considering that function, we can evaluate it at x=3, i.e. find the corresponding value for f(x) when x=-3

`\begin{gathered} f(x)=x^2+8x \\ f(-3)=(-3)^2+8(-3) \\ f(-3)=9-24 \\ f(-3)=-15 \end{gathered}`

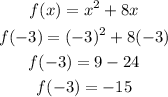
So when we plug x=-3 into that function the corresponding y value is -15

2) Now, the other way around, we've got the y (or f(x)) value -16 let's find the corresponding value for x:

`\begin{gathered} x^2+8x=-16 \\ x^2+8x+16=0 \\ (x+4)^2 \\ x+4=0 \\ x=-4 \end{gathered}`

Note that looking attentively at that trinomial, we can see that this is a binomial (x+4)² or (x+4)(x+4) picking on binomial and equating to zero we can get the root. In this case, there's only value for those two roots x=-4

3) Hence the answer is f(-3)=-15, and x=-4