A rectangular prism has three rectangular faces, and two triangular faces on the top and bottom.
Let the trianglular base has sides a, b, c. And the length of the prism be L.
The Heron's formula can be used to find the area of the base,
![A_1=\sqrt[]{s_1(s_1-a)(s_1-b)(s_1-c)}](https://img.qammunity.org/2023/formulas/mathematics/college/26irq9qdk5x8k2kf47i6lctxpmhc449p0a.png)
Note that 's' is the semiperimeter of the triangular base,
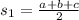
The volume of the prism is then given by,
![\begin{gathered} V_1=A_1* L_{} \\ V_1=\sqrt[]{s(s-a)(s-b)(s-c)}* L \\ 1512=\sqrt[]{s(s-a)(s-b)(s-c)}* L \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/7j4cd72g7exs8pjnnsg7pfn1bdf2wk6oid.png)
Now, consider a new prism whose dimensions are half of the corresponding dimensions of the prism discussed above.
So the triangular base of the new prism has sides a/2, b/2, c/2. And the length of the prism L/2.
Then the area of the triangular base of new prism will be,
![A_2=\sqrt[]{s_2(s_2-(a)/(2))(s_2-(b)/(2))(s_2-(c)/(2))}](https://img.qammunity.org/2023/formulas/mathematics/college/89rpfzhcxlmo5yct4z3h3aonzjlmzebdkc.png)
The relation between the semiperimeters is obtained as,
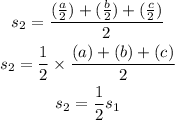
Substitute the value in the area,
![\begin{gathered} A_2=\sqrt[]{((s_1)/(2))((s_1)/(2)-(a)/(2))((s_1)/(2)-(b)/(2))((s_1)/(2)-(c)/(2))} \\ A_2=\sqrt[]{((s_1)/(2))(1)/(2)(s_1-a)(1)/(2)(s_1-b)(1)/(2)(s_1-c)} \\ A_2=\sqrt[]{((1)/(2))^4s_1(s_1-a)(s_1-b)(s_1-c)} \\ A_2=((1)/(2))^2\sqrt[]{s_1(s_1-a)(s_1-b)(s_1-c)} \\ A_2=((1)/(2))^2* A_1 \\ A_2=((1)/(4))^{}* A_1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/egwcijo242wm6qptgsx9nktepp8x54mlcn.png)
Now the volume of this new prism is calculated as,
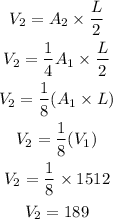
Thus, the volume of the new prism is 189 square feet.
Therefore, option A is the correct choice.