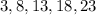Solution:
Given that;
The pattern starts at 3 and adds 5 to each term, i.e.
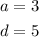
Applying the arithmetic progression formula below

Substitute for a and b into the arithmetic progression formula to find the next term
For the second term, n = 2

For the third term, n = 3
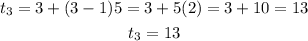
For the fourth term, n = 4

For the fifth term, n = 5
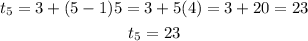
Hence, the first five terms of the sequence are