Question

A photon has a wavelength of 560 nm.  determine the frequency of the photon. calculate the energy of the photon  Where on the electromagnetic spectrum does this photon belong?

Answer 1

Given:

The wavelength of the photon is,

`\begin{gathered} \lambda=560\text{ nm} \\ =560*10^(-9)\text{ m} \end{gathered}`

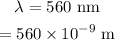
To find:

The frequency, energy, and the position of the photon on the electromagnetic spectrum

Step-by-step explanation:

We know the speed of the electromagnetic wave in a vacuum is,

`c=3*10^8\text{ m/s}`

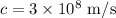
If the frequency of the photon is 'f', we can write,

`\begin{gathered} c=f\lambda \\ f=(c)/(\lambda) \end{gathered}`

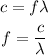
Substituting the values we get,

`\begin{gathered} f=(3*10^8)/(560*10^(-9)) \\ =5.36*10^(14)\text{ Hz} \end{gathered}`

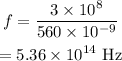
Hence, the frequency of the photon is,

`5.36*10^(14)\text{ Hz}`

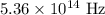
The energy of the photon is,

`\begin{gathered} E=hf \\ h=6.62*10^(-34)\text{ J.s \lparen Planck's constant\rparen} \end{gathered}`

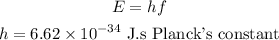
Substituting the values we get,

`\begin{gathered} E=6.62*10^(-34)*5.36*10^(14) \\ =3.55*10^(-19)\text{ J} \end{gathered}`

Hence, the energy of the photon is,

`3.55*10^(-19)\text{ J}`

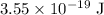
As we know the visible range is,

`400\text{ nm-750 nm \lparen approx\rparen}`

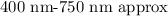
so, the given wavelength belongs to the visible range of the electromagnetic spectrum.