Question

It would be greatly appreciated if you help me answer this question on my worksheet.

Answer 1

Take into account that the total linear momentum must conserve, that it, it is equal before and after the collision:

p_before = p_after

or by using the expression for the momentum p = mv, you have for the given situation:

`m_1v_(1i)+m_2v_(2i)=m_1v_(1f)+m_2v_(2f)_`

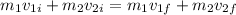
Based on the given information you have:

m1 = 7.05kg

m2 = 1.52kg

v1i = 8.24m/s

v2i = 0m/s

v1f = ?

v2f = 13.2m/s

m1 is the mass of the ball, m2 is the mass of the pin, v1i and v1f makes reference to speed of ball before and after the collision, v2i and v2f makes reference to the speed of pin before and after the collision:

By solving the equation above for v1f, you get:

`v_(1f)=(m_1v_(1i)+m_2v_(2i)-m_2v_(2f))/(m_1)`

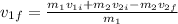
By replacing the values of the parameters:

`\begin{gathered} v_(1f)=((7.05kg)(8.24(m)/(s))+(1.52kg)(0(m)/(s))-(1.52kg)(13.2(m)/(s)))/(7.05kg) \\ v_(1f)\approx5.34(m)/(s) \end{gathered}`

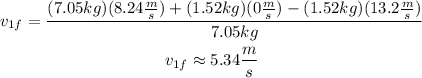
Hence, the speed of the ball after the collision is approximately 5.34m/s