The question gives us an equation and asks us which graph corresponds to the equation.
The equation is the linear equation:
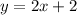
In order to solve this problem, we need to understand the general linear equation.
The general linear equation is given as:
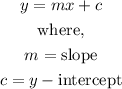
The y-intercept (c), is the point where the graph cuts the y-axis.
Hence, let us compare this general equation to the equation given in the question:

So, we have a slope of 2 and a y-intercept of 2.
This means that the correct graph must cut the y-axis at y = 2.
From observation of the graph, we can make the following observations:
Graph A:
Cuts the y-axis at y = 1. Hence this option is wrong.
Graph B:
Cuts the y-axis at y = 2. It is a possible answer.
Graph C:
Cuts the y-axis at y = 2. It is also a possible answer.
Graph D:
Cuts the y-axis at y = -2. Hence, this option is wrong.
We have two possible options to choose from: Graph B and Graph C.
Now, we need to choose which one is the accurate one.
To find out, we need to calculate the value of the slope (m). The slope must be m = 2.
The formula for slope is given below:
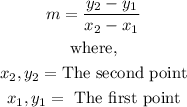
Let us examine the graphs below:
Graph C:
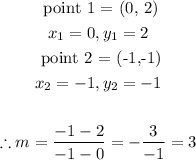
The slope of Graph C is 3. Hence, it cannot be the answer.
This means Graph B is likely the answer but let us confirm.
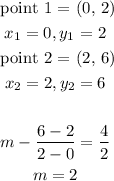
The slope of Graph B is 2.
Thus, we can confirm that the answer is Option B