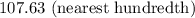Question

z varies directly as x and inversely as y. If z = = 123 when x = 6 and y = 6, find z if x = 7 and y = 8.(Round off your answer to the nearest hundredth.)=

Answer 1

Given that z varies directly as x and inversely as y, this is expressed mathematically as

`z\propto x\propto(1)/(y)`

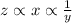
Introducing a proportionality constant k, we have

`\begin{gathered} z=k(x)/(y) \\ \Rightarrow k=(zy)/(x)\text{ ---- equation 1} \end{gathered}`

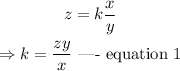
When z = 123, x=6, and y=6 , k is evaluated to be

`\begin{gathered} k=(zy)/(x)\text{ } \\ =(123*6)/(6) \\ \Rightarrow k=123 \end{gathered}`

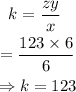
Thus, equation 1 becomes

`123=(zy)/(x)`

To evaluate z when x =7 and y=8, we substitute the respective values of x and y into the above equation.

Thus,

`\begin{gathered} 123=(zy)/(x) \\ \Rightarrow123=(z*8)/(7) \\ \text{make z the subject of the formula} \\ z*8=123*7 \\ \text{divide both sides by 8} \\ (z*8)/(8)=(123*7)/(8) \\ z=(123*7)/(8) \\ =\: 107.625 \\ \Rightarrow z\approx107.63\text{ (nearest hundredth)} \end{gathered}`

Hence, the value of z when x =7 and y =8 is

`107.63\text{ (nearest hundredth)}`