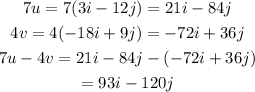Question

Vector vector u equals vector PQ has initial point P (5, 16) and terminal point Q (8, 4). Vector vector v equals vector RS has initial point R (28, 7) and terminal point S (10, 16).

Answer 1

PART A:

The linear form of a vector is given by:

`y=ai+bj`

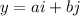
Where i indicates the horizontal direction and j indicated the vertical direction.

To find the values of a and b, let's find the horizontal and vertical distances between the points.

For vector u, we have:

`\begin{gathered} Q_x-P_x=8-5=3 \\ Q_y-P_y=4-16=-12 \\ u=3i-12j \end{gathered}`

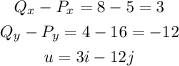
For vector v, we have:

`\begin{gathered} S_x-R_x=10-28=-18 \\ S_y-R_y=16-7=9 \\ v=-18i+9j \end{gathered}`

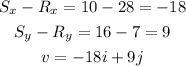
PART B:

To find the trigonometric form, we need the magnitude and angle of each vector:

`\begin{gathered} \text{ vector u:} \\ |u|=\sqrt[]{3^2+(-12)^2}=\sqrt[]{9+144}=\sqrt[]{153} \\ \theta=\tan ^(-1)((-12)/(3))=-75.96\degree \\ u=\sqrt[]{153}(\cos (-75.96\degree)i+\sin (-75.96\degree)j) \\ \text{vector v:} \\ |v|=\sqrt[]{(-18)^2+9^2_{}}=\sqrt[]{324+81}=\sqrt[]{405} \\ \theta=\tan ^(-1)((9)/(-18))=-26.57\degree \\ v=\sqrt[]{405}(\cos (-26.57\degree)i+\sin (-26.57\degree)j) \end{gathered}`

PART C:

Calculating the given operation, we have:

`\begin{gathered} 7u=7(3i-12j)=21i-84j \\ 4v=4(-18i+9j)=-72i+36j \\ 7u-4v=21i-84j-(-72i+36j) \\ =93i-120j \end{gathered}`