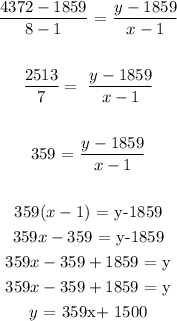Question

The table below represents the total cost of leasing a car at the end of each month. Write an equation in slope-intercept slope form to represent the cost, y, of leasing a car for x months.

Answer 1

`y\text{ = 359x + 1500}`

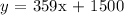
Step-by-step explanation:

Here, we want to write an equation in slope-intercept form

What we need to do is to select two points to use, then apply the two-points form

We have that as:

`(y_2-y_1)/(x_2-x_1)\text{ = }(y-y_1)/(x-x_1)`

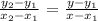
We pick any two points as (x1,y1) and (x2,y2)

We have that as:

(1,1859) and (8,4372)

Substituting the values, we have it that:

`\begin{gathered} (4372-1859)/(8-1)\text{ = }(y-1859)/(x-1) \\ \\ (2513)/(7)=\text{ }(y-1859)/(x-1) \\ \\ 359\text{ = }(y-1859)/(x-1) \\ \\ 359(x-1)\text{ = y-1859} \\ 359x-359\text{ = y-1859} \\ 359x-359+1859\text{ = y} \\ 359x-359+1859\text{ = y} \\ y\text{ = 359x+ 1500} \end{gathered}`