Given:

To Determine: The volume of the empty portion of container B
Solution
The container is in the shape of a cylinder. The volume of a cylinder can be calculated as shown below
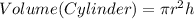
So,
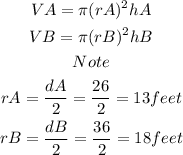
Let us substitute the given into the formula
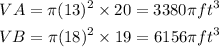
The volume of the empty portion of container B would be
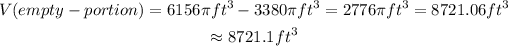
Hence, the volume of the empty portion of conatiner B is approximately 8721.1 cubic foot