Given:
f(x) = 2Ln(x)
x1 = 9
Let's find the slope given different values of x2.
Apply the formula:
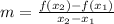
• When x2 = 14.
First find the value of f(x) when x = 9.
Substitute x for 9 in f(x) and solve.
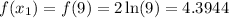
Now, solve for f(x) when x = 14:
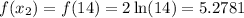
To find the slope, subtitute 4.3944 for f(x1), 5.2781 for f(x2), 9 for x1, and 14 for x2 in the slope formula and solve for m.
Thus, we have:
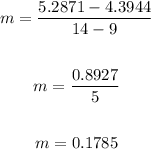
When x2 = 14, m = 0.1785
• When x2 = 11
Using the same method used in the first part above, we have:
f(x1) = 4.3944
To solve for f(x2), substitute 11 for x:
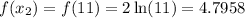
Now, to find the slope, we have:
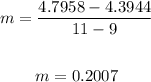
When x2 = 11, m = 0.2007
• When x2 = 10:
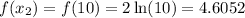
To find the slope, we have:
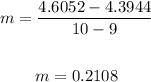
When x2 = 10, m = 0.2108
• When x2 = 9.1
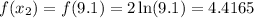
To find the slope, we have:
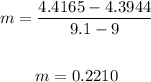
When x2 = 9.1, m = 0.2210
• When x2 = 9.01:
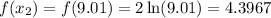
To find the slope, we have:
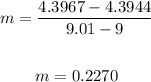
When x2 = 9.01, m = 0.2270
ANSWER:
• When x2 = 14, m = , 0.1785
,
• When x2 = 11, m = , 0.2007
,
• When x2 = 10, m = , 0.2108
,
• When x2 = 9.1, m = , 0.2210
,
• When x2 = 9.01, m = , 0.2270