Starting with the equation:

Take the expression on the right hand side of the equation:
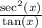
From the Pythagorean Identity and the definition of secant, we can prove that:
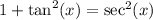
That fact can be verified as follows: the Pythagorean Identity states that:
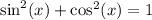
Divide both sides by the squared sine of x: