Question

A company makes Citi bikes. 95% (i.e., 0.95) pass final inspection. Suppose that 5 bikes are randomly selected. ( use binomial distribution formula).a)What is the probability that exactly 4 of these 5 sports bikes pass final inspection?b)What is the probability that less than 3 of these 5 sports bikes pass final inspection? Please help asap am I suppose use binomial distribution formula. Am I supposed to use the factorial symbol that looks like an ! exclamation point Please help me understand this part a and b

Answer 1

Step-by-step explanation

We can find the solution to Part A and B using the binomial distribution formula below.

`(nCx)p^xq^(n-x)`

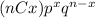
n= number of random bikes selected=5

x= desired number

p= probability of success= 0.95

q= probability of failure =1-0.95 =0.05

Part A

For exactly 4 out of 5 passing the inspection, we will have;

`\begin{gathered} Pr(x=4)=5C4(0.95)^4(0.05)^1 \\ =(5!)/(4!1!)(0.95)^4(0.05) \\ =5(0.95)^4(0.05)=0.2036 \end{gathered}`

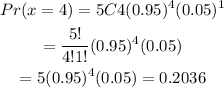
Answer: 0.2036

Part B

For the probability that less than 3 of these 5 sports bikes pass final inspection

`Pr(x<3)=Pr(0)+Pr(1)+Pr(2)`

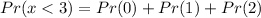
Therefore, we will have

`\begin{gathered} Pr(0)=(5!)/(5!0!)(0.95)^0(0.05)^5=0.05^5 \\ Pr(1)=(5!)/(1!4!)(0.95)^1(0.05)^4=5(0.95)(0.05)^4 \\ Pr(2)=(5!)/(2!3!)(0.95)^2(0.05)^3=10(0.95)^2(0.05)^3 \\ Pr(x<3)=0.05^5+5(0.95)(0.05)^4+10(0.95)^2(0.05)^3 \\ =0.001158 \end{gathered}`

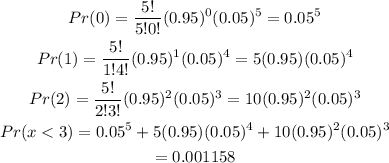
Answer: 0.001158