How to solve y=2x+3 y=2x+1

Question

asked Mar 9, 2023 154k views

1 Answer

Sayed Sohan · Answer 1 · 2023-03-15T08:42:17+0000

We have the system of equations

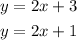
$\begin{gathered} y=2x+3 \\ y=2x+1 \end{gathered}$

Using substitution, we have that

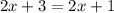
Solving for x, we have that

$\begin{gathered} 2x-2x=1-3 \\ 0=-2 \end{gathered}$

but this is a contradiction, therefore the system of equations don't have a solution.

We also can notice this if we graph the equations.

From the graph we see that the equations do not intersect, then the system don't have a solution.