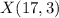Given the coordinates of T, U and V as;
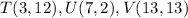
The midpoint of UV is W, which is;
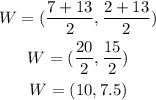
Also, W is collinear and between T and X;
Sketching the graph here for clarity, we have;
Also, TX is exactly two times TW;
That means, W is the midpoint of TX, we have;
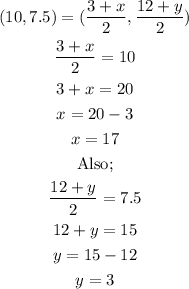
Hence, the coordinate of X is;