Type 1
this is a right triangle, the we can apply pythagoras
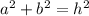
where a and b are sides and h the hypotenuse on this case L(leash)
replacing
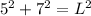
simplify
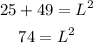
now solve for L
![L=\sqrt[]{74}\approx8.6](https://img.qammunity.org/2023/formulas/mathematics/high-school/uc8ghfsgo3imnwg3yr8raingh9o4p1twyz.png)
The leash is 8.6ft
Type 2
we have a right triangle too
on this case the missing number is a side, not hypotenuse
remember pythagoras
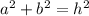
and replace for this case
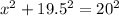
simplify
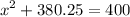
and solve for x
![\begin{gathered} x^2=19.75 \\ x=\sqrt[]{19.75}\approx4.44 \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/oubvjsppwfm1mthdna1zp4a6aym96pdv4x.png)
then le length of the side x is 4.44ft