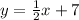Solution:
The solution given in the question is given below as
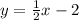
The coordinates given in the question are
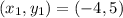
Concept:
The general formula of an equation of a line in slope-intercept form is given below as
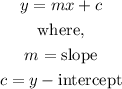
By comparing coeficient,
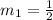
Note:
Two lines are said to be parallel if they have the same slope
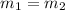
Therefore,
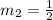
The formula used to calculate the equation of a line is given below as
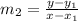
By substituting the values, we will have
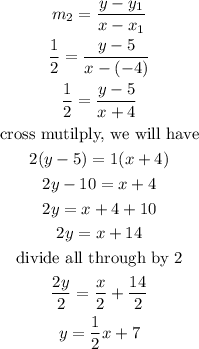
Hence,
The final answer is