A) Use the following formula for the linear expansion, in this case, of the diameter of the spherical ball:
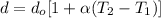
where,
do: initial diameter = 11.21cm
d: final diameter = ?
α: linear expansion coefficient = 24*10^6 /°C
T2: final temperature = 257°C
T1: intial temperature = 33°C
Replace the previous values of the parameters into the formula for d and simplify:
Hence, the diameter of the spherical ball is 11.27cm
B) First, consider what is the change in the radius of the sphere, as follow:

Now, use the following formula for the change in volume with the temperature:

where you have used the equivalence β = 3α.
Solve the equation above for the change in temperature and replace the values of the other parameters:
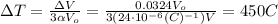
Hence, the change in temperature is 450°C