Given the two-way table, let's find the probability that a student selected at random is a junior student given that it's male.
Total number of students = 4 + 6 + 2 + 2 + 3+ 4 + 6 + 3 = 30
Number of male students = 4 + 6 + 2 + 2 = 14
Number of female students = 3 + 4 + 6 + 3 = 16
To find the probability that a randomly selected student is a junior given that the student is male, we have:

Where:
Number of male junior students = 2
Number of male students = 14
Thus, we have:
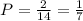
To write the probability as a percentage, multiply by 100:

Therefore, the probability that a randomly selected student is a junior given that it's male is 14%
A