Answer:
3.34
Step-by-step explanation:
The relationship between final angular speed, initial angular speed, angular acceleration, and change in radians is given by
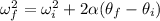
Now in our case
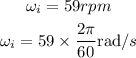
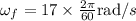
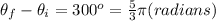
Therefore, the above equation gives
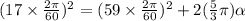
subtracting (17 2pi/ 60 )^2 from both sides gives
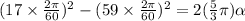
dividing both sides by 2 * 5 / 3 pi gives
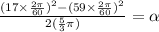
simplifying the above gives
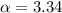
which is our answer!