To solve this question, follow the steps below.
Step 01: Factor out "x".
Given:
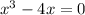
Since both terms have "x", you can factor out "x":

Step 02: Find the values of x.
In order to the result be zero, or x = 0, or (x² - 4) = 0.
First, do x = 0.
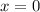
Second, do (x² - 4) = 0.
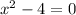
To find x, add 4 to both sides of the equation.
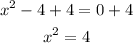
And take the root of both sides.
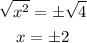
Answer: x = -2, 0, 2.