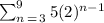Step 1. The sequence that we have in the table is:
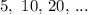
As you can see the number doubles each time.
We require to find the expression that represents the sum for term 3 through term 9 in sigma notation.
Step 2. First, since the summation has to be from term 3 to term 9, the sigma notation should look as follows:

This discards options 1 and 3.
Step 3. Now we need to find an expression that represents the sum of the terms. If we continue the sequence the numbers would be:
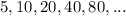
We can also express this as 5 multiplied by a power of 2:
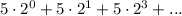
That is because
2^0=1
2^1=2
2^2^4
.
.
.
Therefore, the result of the multiplications:
![undefined]()
This can be simplified to:
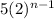
Step 4. The final expression is:
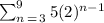
Which is shown in the second option.
Answer: