SOLUTION
Write out the expression
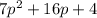
Step1; Multiply the first and the last term
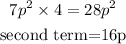
Step2: Obtain the factors of that completely replace the product and the second term above
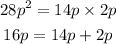
Step3: Replace the second term with the factors you obtained above
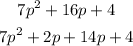
Step4: Break the expression into groups
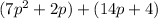
Step5: Factor the expression in paranthesis
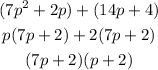
Hence
The complete factor of the trinomial is (7p+2)(p+2)