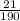Solution:
The probability of an event is expressed as
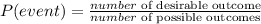
Given that:
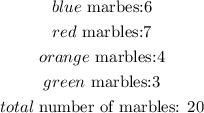
This implies that the number of possible outcomes is 20.
Provided that once a marble is drawn, it's replaced, the probability of selecting a red marble then a blue marble is expressed as

where

Thus, we have
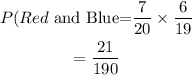
Hence, the probability of selecting a red then a blue marble is