Question

I have to finish this assignment today! I need help solving these questions.Solve 8

Answer 1

We have a square

`EF=10\sqrt[]{2}`

we can use the Pythagorean theorem in order to find y

`3y+11=\sqrt[]{(10\sqrt[]{2})^2+(10\sqrt[]{2})^2}=20`

then we clear y

`\begin{gathered} 3y+11=20 \\ 3y=20-11 \\ 3y=9 \\ y=(9)/(3) \\ y=3 \end{gathered}`

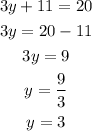
In order to find x, we need to remember the interior angles of a square are equals to 90° and the diagonals divided this angle into equal angles in other words the value is 45°

so we have the next equation

`7x-25=45`
`\begin{gathered} 7x=45+25 \\ 7x=70 \\ x=(70)/(7) \\ x=10 \end{gathered}`

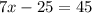
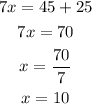
the value of x=10