Question

Write an equation that is perpendicular to y=-4x-6 and passes through the point (4,10).

Answer 1

Consider that the standard equation of a line with slope (m) and y-intercept (c) is given by,

`y=mx+c`

Comparing with the given equation, the slope is obtained as,

`m=-4`

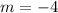
Let m' be the slope of the perpendicular line.

The line will be perpendicular only if their product of slopes is -1,

`\begin{gathered} m* m^(\prime)=-1 \\ -4* m^(\prime)=-1 \\ m^(\prime)=(-1)/(-4) \\ m^(\prime)=(1)/(4) \end{gathered}`

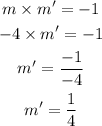
So the equation of this perpendicular line is given by,

`y=(1)/(4)x+c^(\prime)`

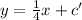
Since the perpendicular if at point (4,10), so it must satisfy its equation,

`\begin{gathered} 10=(1)/(4)(4)+c^(\prime) \\ 10=1+c^(\prime) \\ c^(\prime)=9 \end{gathered}`

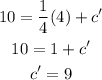
Substitute the value back in the equation,

`\begin{gathered} y=(1)/(4)x+9 \\ 4y=x+36 \\ x-4y+36=0 \end{gathered}`

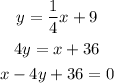
Thus, the required equation which is perpendicular to the given line is x-4y+36=0.