Question

Between 1990 and 1999, the number of movie screens increased by 1500 per year. There were 20690 movie screens in 1990. Use a linear model to (a) determine how many movie screens there were in 1995 and (b) in what year were there 32690 movie screens.-use a representation to organize though (table,diagram,chart ,graphs,number order, etc)-use written and verbal explanation of what was done that justified each step-use more than one strategy that would show it is correct

Answer 1

a)in 1995 there were 28910 screens

b)in 1998 there were 32690 movie screens

Step-by-step explanation

the equation of a lines can be writen as

`\begin{gathered} y=mx+b \\ where\text{ m is the slope} \\ and\text{ b is th ey-intercept} \end{gathered}`

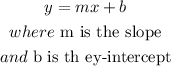
so, for the problem,

let

`\begin{gathered} slope=rate\text{ per year=}1500 \\ b=\text{ initial amount=}20690 \end{gathered}`

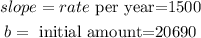
now, replace

`\begin{gathered} y=1500x+20690 \\ whre\text{ x represents the number of years after 1990} \\ y\text{ represents the number of movie screens there were} \end{gathered}`

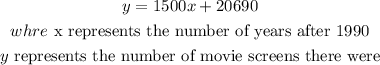
so

Step 1

a)how many movie screens there were in 1995 and

i) find the x value

`x=\text{ 1995-1990=5}`

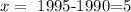
ii) replace in the equation

`\begin{gathered} y=1500x+20690 \\ y=1500\left(5\right)+20690 \\ y=7500+20690 \\ y=28190 \end{gathered}`

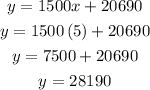
hence

in 1995 there were 28910 screens

Step 2

(b) in what year were there 32690 movie screens.

Let

`y=32690`

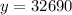
replace in the equation and solve for x

`\begin{gathered} y=1500x+20690 \\ 32690=1500x+20690 \\ subtract\text{ 20690 in both sides} \\ 32690-20690=1500x+20,690-20690 \\ 12000=1500x \\ divid\text{e both sides by 1500} \\ (12,000)/(1500)=(1,500x)/(1500) \\ 8=x \end{gathered}`

finally, add 1990 to know the year

`year\text{ =}1990+8=1998`

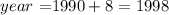
so

b) in 1998 there were 32690 movie screens

I hope this helps you