Given: The equation and inequalty below
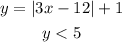
To Determine: The values of x satisfying the given conditions using interval notation
Solve the first equation
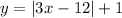
![\mathrm{Domain\: of\: }\: \mleft|3x-12\mright|+1\: \colon\quad \begin{bmatrix}\mathrm{Solution\colon}\: & \: -\infty\: The range[tex]\mathrm{Range\: of\: }\mleft|3x-12\mright|+1\colon\quad \begin{bmatrix}\mathrm{Solution\colon}\: & \: f\mleft(x\mright)\ge\: 1\: \\ \: \mathrm{Interval\: Notation\colon} & \: \lbrack1,\: \infty\: )\end{bmatrix}]()
The y-intercept, make x = 0

The minimum point

Let us graph the two equation as shown below
From the graph above, the set of values of x that satisfies the equation and inequality can be seen from point A to point B.
Hence,
The solution is 2.667 < x < 5.333
Using interval notation we have (2.667, 5.333)