Solution
Question A
- The formula representing the growth/decay rate of the function is given by:
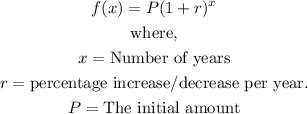
- Comparing this formula with the function given, we have:
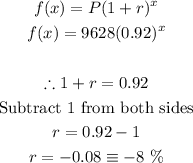
- The rate is a negative rate, thus, we can conclude that the amount in Account A is Decreasing and it's decreasing at 8% per year.
Question B
- The formula we will use to find the rate of change from year to year is:
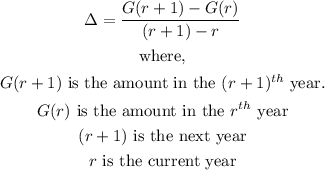
- We can simplify the formula further as follows:
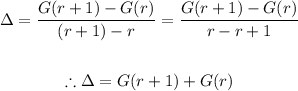
- Now, let us apply the formula to solve the question:

- The question we are asked to solve for Question B is vague. I cannot proceed from here.
Final Answer
Question A
The rate is a negative rate, thus, we can conclude that the amount in Account A is Decreasing and it's decreasing at 8% per year.