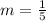Question

(13, -2), (-2,-3) find the slope of the line

Answer 1

The slope of a line can be calculated with the following formula:

`m=(y_2-y_1)/(x_2-x_1)`

In this case, given these points:

`\mleft(13,-2\mright);(-2,-3)`

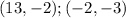
You can set up that:

`\begin{gathered} y_2=-3 \\ y_1=-2 \\ x_2=-2 \\ x_1=13 \end{gathered}`

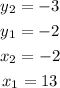
Knowing these values, you can substitute them into the formula and then evaluate, in order to find the slope of the line. This is:

`\begin{gathered} m=(-3-(-2))/(-2-13) \\ \\ m=(-3+2)/(-15) \\ \\ m=(-1)/(-15) \\ \\ m=(1)/(5) \end{gathered}`

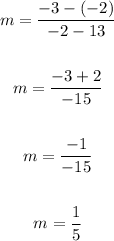
The slope is:

`m=(1)/(5)`