Solution
- The formula for finding the discriminant using the formula below:
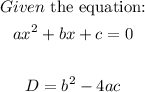
- The equation given to us is:
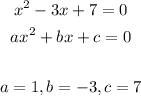
- Thus, the discriminant is:
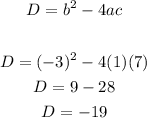
- The discriminant is negative. We can make the following inferences based on the discriminant:
1. If the discriminant (D) > 0, then the equation has 2 real solutions
2. If the discriminant (D) = 0, then, the equation has 1 real root.
3. If D < 0, then, the equation has no real roots.
- We have a negative discriminant, meaning that D < 0.
- Thus the roots are complex
Final Answer
The answer is "2 complex roots"