1 Answer

Akshaya Aradhya · Answer 1 · 2023-03-30T03:35:30+0000

Solution

- The formula for finding the discriminant using the formula below:

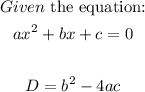
$\begin{gathered} Given\text{ the equation:} \\ ax^2+bx+c=0 \\ \\ D=b^2-4ac \end{gathered}$

- The equation given to us is:

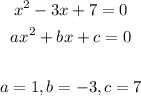
$\begin{gathered} x^2-3x+7=0 \\ ax^2+bx+c=0 \\ \\ a=1,b=-3,c=7 \end{gathered}$

- Thus, the discriminant is:

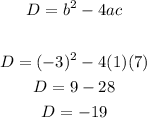
$\begin{gathered} D=b^2-4ac \\ \\ D=(-3)^2-4(1)(7) \\ D=9-28 \\ D=-19 \end{gathered}$

- The discriminant is negative. We can make the following inferences based on the discriminant:

1. If the discriminant (D) > 0, then the equation has 2 real solutions

2. If the discriminant (D) = 0, then, the equation has 1 real root.

3. If D < 0, then, the equation has no real roots.

- We have a negative discriminant, meaning that D < 0.

- Thus the roots are complex

Final Answer

The answer is "2 complex roots"

Please log in or register to add a comment.