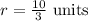Given: An sector with a central angle-
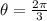
And area,
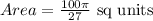
Required: To determine the radius of the sector.
Explanation: The area of the sector when the central angle is in radians is given by the formula-
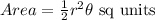
Substituting the values into the formula as-

Further solving for 'r' as follows-

Final Answer: The radius of the sector is-