Question

The pair of figures are similar. Use the information given to find the scale factor of the figure on the left to the figure on the right.V = 576 mi³V = 9000 mi³SF =

Answer 1

When two figures are similar, the scale factor is given by the ratio between the measure of two corresponding lengths of the two figures.

`r\propto R\implies R=kr`

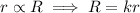
Where k represents the scale factor.

Since the volume is a three dimensional measure(it is the product of three length units), the ratio between the volumes is the scale factor to the third power

`R=kr\implies R^3=(kr)^3=k^3r^3\implies(R^3)/(r^3)=k^3`

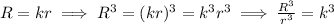
Then, in our problem, the ratio between the volumes is:

`(576)/(9000)=0.064`

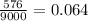
Then, the scale factor is the cubic root of this ratio:

`\sqrt[3]{0.064}=0.4`

The scale factor is 0.4.