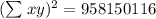EXPLANATION
Assuming the given table, we can compute the calculations as shown as follows;
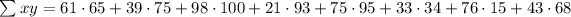
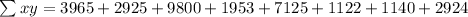
Adding terms:
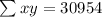
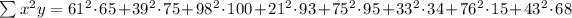
Computing the powers:
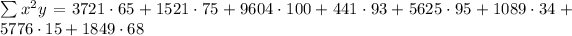
Multiplying terms:
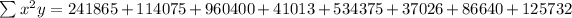
Adding terms:
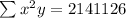
Now, we need to compute the third equation:
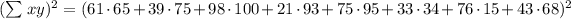
Multiplying terms:
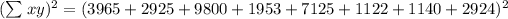
Adding numbers:
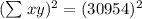
Computing the power: