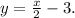System A:
Notice that:
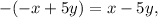
therefore the first system of equations implies that:
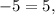
the above result is a contradiction, therefore system A has no solution.
System B:
Notice that:
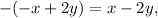
therefore the second system of equations implies that:
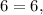
then the second system has infinitely many solutions, they must satisfy:
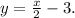
Answer:
System A: The system has no solution.
System B: The system has infinitely many solutions, they must satisfy: