The exercise tells us that the electric field is given by the following equation:
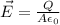
And it also gives us, A and Q. Thus, our electric field inside the capacitor is:
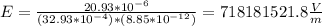
As we know, the electric force can be written as:
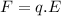
The charge of an electron is a constant, which is q=1.6*10^(-19) C.
Finally, our force can be written as:
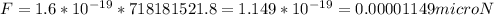
Our final answer is 0.00001149 micro Newtons