Question

g=10m/s^2The diagram shows a box of mass m = 24 kg and three ropes that are part of a system in equilibrium. The slanted rope makes an angle = 37° with the horizontal. Determine expressions for each of the following:(a) The tension in the slanted rope, T1(N)(b) The tension in the horizontal rope, T2(N)

Answer 1

Given,

The mass of the box, m=24 kg

The acceleration due to gravity, g=10 m/s²

The angle made by slanted rope, θ=37°

As the system is in equilibrium, there is no net force acting on the mass.

(a) Therefore, the y-component of the tension T₁ will be equal to the weight of the box.

That is,

`T_1\sin \theta=mg`

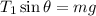
Thus,

`T_1=(mg)/(\sin \theta)`

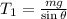
On substituting the known values,

`\begin{gathered} T_1=(24*10)/(\sin 37^(\circ)) \\ =398.8\text{ N} \end{gathered}`

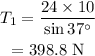
Thus the tension T₁ is 398.8 N

(b) As the system is in equilibrium the net force is zero in x-direction too.

Thus the x-component of tension T₁ will be equal to T₂

That is,

`T_2=T_1\cos \theta`

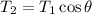
On substituting the known values,

`\begin{gathered} T_2=398.8*\cos 37^(\circ) \\ =318.5\text{ N} \end{gathered}`

Thus the tension T₂ is 318.5 N